Transformers

$\newcommand{\abs}[1]{\left\lvert#1\right\rvert}$ $\newcommand{\norm}[1]{\left\lVert#1\right\rVert}$ $\newcommand{\inner}[1]{\left\langle#1\right\rangle}$ $\DeclareMathOperator*{\argmin}{arg\,min}$ $\DeclareMathOperator*{\argmax}{arg\,max}$ $\DeclareMathOperator*{\E}{\mathbb{E}}$ $\DeclareMathOperator*{\V}{\mathbb{V}}$ $\DeclareMathOperator*{\x}{\mathbb{x}}$

ransformers consist of two stacks – an encoder stack and a decoder stack. Each of these stacks is composed of $N=6$ identical layers that sequentially feed into each other.

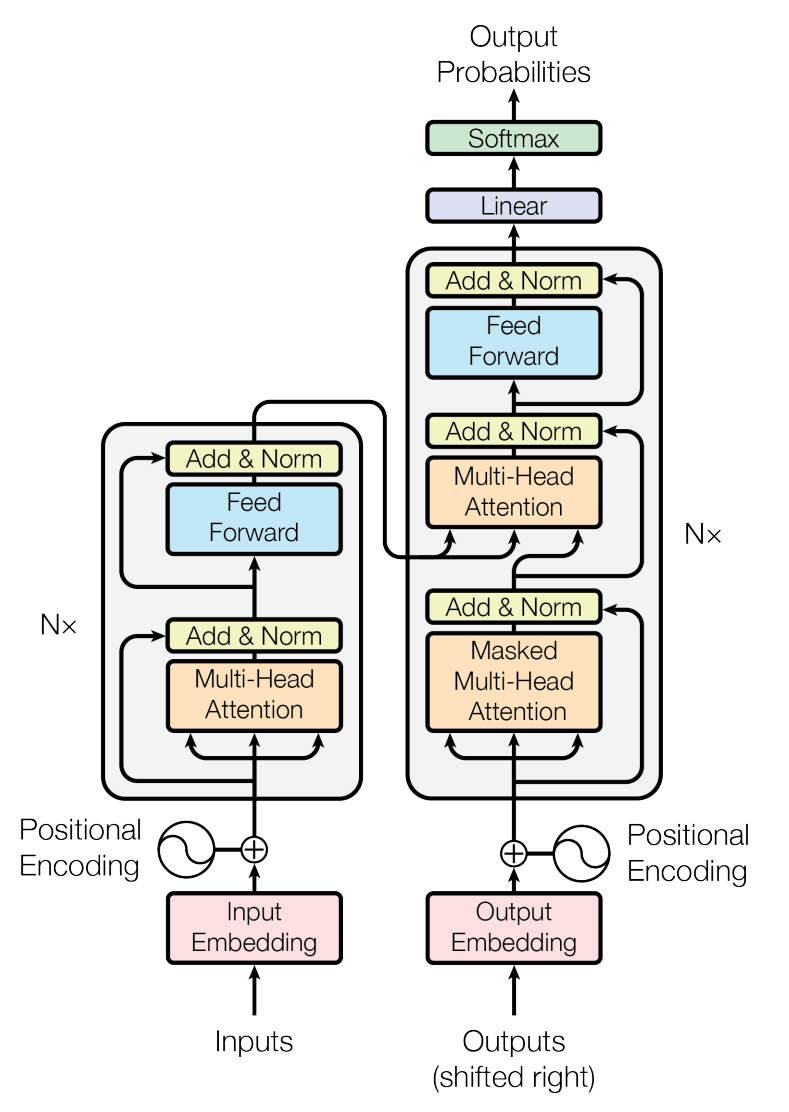
Tranformer Architecture proposed in 'Attention Is All You Need'

Each layer in encoder has two sub-layers,

multi-head self-attention block,
feedforward neural network block,
residual connection around each of the sub-layers, followed by layer normalization, i.e., each sub-layer outputs $LayerNorm(x+Sublayer(x))$.

Each layer in decoder has three sub-layers,

multi-head masked self-attention block (masking ensures that predictions can only use the past information),
feedforward neural network block,
multi-head cross-attention block (takes encoder output key & value but its own query),
residual connection around each of the sub-layers, followed by layer normalization,

Finally, decoder output is linearly transformed to convert the predictions back from the embedding space and softmax is applied to generate the probability distribution.

Notation: $n: = n_{seq}$ – sequence length (elements in input sequence). $d_{model}$ – embedding dimension. $h := n_{heads}$ – number of heads. $d_k = d_q := d_{model}/n_{heads}$ – key (query) matrix dimension. $d_v := d_{model}/n_{heads}$ – value matrix dimension.

Embeddings

Embeddings are not a novel idea, e.g., they were already used in word2vec representations in 2013. But word2vec embeddings were static and wound not change depending on the context, e.g., some words have different meaning depending on the context – a bat could be an animal or a wooden object. To pass in the context, it is essential to encode the contextual information into the embedding. RNN tackled this by encoding this context that was then passed as input to decoder. However, this contextual signal was not strong enough to persist in longer sentences, and so attention was introduced sometime in 2014-2015.

Instead of one-hot encoding words (or its pieces), Transformers encode words with embeddings. Namely, words are first mapped to integers (e.g., label encoded), and then these integers are mapped into some (initially random) points in $d_{model}$-dimensional space. Embeddings effectively act as a dictionary between this label encoded value and a vector in $d_{model}$ space. Hence each word is represented by a vector and this vector will be learned during training.

class Embeddings(nn.Module):
    def __init__(self, d_model: int, vocab: int):
        super().__init__()
        self.d_model = d_model
        self.vocab = vocab
        self.embedding = nn.Embedding(vocab, d_model)

    def forward(self, x):
        return self.embedding(x) * math.sqrt(self.d_model)

Positional Encodings

Neither embeddings nor attention have notion of space, i.e., they do not provide information about the relative position of the token in a sequence. Positional Encodings (PE) allow to inject this information and are crucial for modeling sequential data. PEs also allow the data to be processed in parallel, thus solving the bottleneck issue that RNNs and LSTMs had.

PEs have the same dimension as embedding, $d_{model}$, and are simply summed with the embedding vectors to pass in the positional information. Though as opposed to learnable embeddings, PEs are not learned during training (at least in the original 2017 implementation).

There are different ways to encode the positional information, but the original paper uses sin and cos functions,

\[PE(pos, 2i) = \sin\left(\frac{pos}{10000^{2i/d_{model}}}\right),\] \[PE(pos, 2i+1) = \cos\left(\frac{pos}{10000^{2i/d_{model}}}\right),\]

where $pos$ is the token’s position in the sequence and $i=0, \ldots, d_{model}-1$ refers to the embedding dimension. The wavelength ranges from $2\pi$ for the first embedding dimension to $10000\times 2\pi$ for the last embedding dimension.

Plot below shows PEs across $n=20$ tokens and $d_{model}=32$ embedding dimension.

In the code implementation below we have,

dropout added to the sum of Embeddings and PEs (in the original paper dropout prob is set to 0.1),
the argument inside the sinusoid is computed in log space to avoid numerical issues, $(pos \times e^{-2i \log(10000)/d_{model}})$.

class PE(nn.Module):
    def __init__(self, d_model: int, seq_len: int, dropout: float):
        super().__init__()
        self.d_model = d_model
        self.seq_len = seq_len
        self.dropout = nn.Dropout(dropout)

        pe = torch.zeros(seq_len, d_model)
        position = torch.arange(0, seq_len, dtype=torch.float).unsqueeze(1)
        div_term = torch.exp(
            torch.arange(0, d_model, 2).float() * (-math.log(10_000.0) / d_model)
        )
        pe[:, 0::2] = torch.sin(position * div_term)
        pe[:, 1::2] = torch.cos(position * div_term)
        pe = pe.unsqueeze(0)  # (1, seq_len, d_model)
        self.register_buffer("pe", pe)  # saved as a (nonlearnable) variable

    def forward(self, x):
        x = x + (self.pe[:, : x.shape[1], :]).requires_grad_(False)
        return self.dropout(x)

Multi-head attention

Embeddings and PEs are summed, and 4 copies are made. As can be seen in the transformer architecture graph above, three copies are passed into Encoder’s Multi-Head (self-)Attention layer, whereas the fourth copy is passed into Add & Norm layer. Since the attention is multi-head, each of the 3 copies gets partitioned into $h$ parts across the embedding dimension. Attention mechanism is the key component of transformer architecture and is discussed in the previous post.

In the original transformer, there are 3 places where attention is computed:

self-attention in encoder,
(masked) self-attention in decoder,
cross-attention (Q from decoder mixed with K & V from encoder) in decoder.

class MultiHeadAttention(nn.Module):
    def __init__(self, d_model: int, n_heads: int, dropout: float):
        super(MultiHeadAttention, self).__init__()
        self.d_model = d_model
        self.n_heads = n_heads
        self.d_k = d_model // n_heads

        assert self.d_k * n_heads == d_model, "d_model must be divisible by n_heads"

        self.W_q = nn.Linear(d_model, d_model)
        self.W_k = nn.Linear(d_model, d_model)
        self.W_v = nn.Linear(d_model, d_model)
        self.W_o = nn.Linear(d_model, d_model)

        self.dropout = nn.Dropout(dropout)
        self.attention = ScaledDotProductAttention()

    def forward(
        self, query: Tensor, key: Tensor, value: Tensor, mask: Tensor = None
    ) -> Tensor:

        batch = query.shape[0]
        Q = self.W_q(query)  # -> (batch, seq_len, d_model)
        K = self.W_k(key)  # -> (batch, seq_len, d_model)
        V = self.W_v(value)  # -> (batch, seq_len, d_model)

        # -> (batch, n_heads, seq_len, d_k)
        Q = Q.view(batch, -1, self.n_heads, self.d_k).transpose(1, 2)
        K = K.view(batch, -1, self.n_heads, self.d_k).transpose(1, 2)
        V = V.view(batch, -1, self.n_heads, self.d_k).transpose(1, 2)

        out, self.attention_weights = self.attention(Q, K, V, mask, self.dropout)

        # -> (batch, seq_len, d_model)
        out = out.transpose(1, 2).contiguous().view(batch, -1, self.d_model)

        return self.W_o(out)

Layer Normalization

Layer normalization is essential for stabilizing and improving learning. Unlike batch normalization, which normalizes across the batch dimension (per feature), layer normalization normalizes across the feature dimension (per sample). In its simplest form, the output of layer normalization for vector $\x \in \mathbb{R}^{d_{model}}$ is computed as,

\[\hat{x}_i = \frac{x_i - \hat{\mu}}{\hat{\sigma} + \epsilon},\]

where $\hat{\mu}$ and $\hat{\sigma}$ are the mean and standard deviation calculated over $d_{model}$ dimensions. This normalization may be too restrictive, so in practice it is common to add a multiplicative and additive learnable parameters, i.e., the output becomes $\gamma \hat{x}_i + \beta$.

class LayerNorm(nn.Module):
    def __init__(self, d_model, eps: float = 1e-6):
        super(LayerNorm, self).__init__()
        self.eps = eps
        self.gamma = nn.Parameter(torch.ones(d_model))
        self.beta = nn.Parameter(torch.zeros(d_model))

    def forward(self, x):
        mean = x.mean(dim=-1, keepdim=True)
        std = x.std(dim=-1, keepdim=True)
        return self.gamma * (x - mean) / (std + self.eps) + self.beta

Residual Connection

As seen in transformer architecture plot, layer normalization in encoder happens after multi-head attention computation and also after feedforward neural network layer. In both cases there is also a residual connection for improving training and protecting against vanishing (and exploding) gradients. Residual connection implies passing the sum of the input and the output of the attention block to the following layer, i.e., $x \leftarrow x + \text{multiheadattention}(x, x, x)$.

class ResidualConnection(nn.Module):
    def __init__(self, d_model: int, dropout: float):
        super().__init__()
        self.dropout = nn.Dropout(dropout)
        self.norm = LayerNorm(d_model)

    def forward(self, x, sublayer):
        return x + self.dropout(sublayer(self.norm(x)))

Notice that in the paper (and in the transformer plot) layer normalization happens after the residual connection, however in the code above this order is switched – we first normalize and then add the residual connection. Most available code implementation stick with this approach.

Feedforward Net

The output of the multi-head attention block is passed to good old feedforward neural network. The original paper uses 2-layer network with dropout and relu,

\[\text{FFN}(\x) = \max(0, \x W_1 + b1) W_2 + b_2,\]

with $W_1 \in \mathbb{R}^{d_{model}\times d_{ff}}$, $W_2 \in \mathbb{R}^{d_{ff}\times d_{model}}$ and $d_{ff}=2048$.

class FeedForwardNetwork(nn.Module):
    def __init__(self, d_model: int, d_ff: int = 2048, dropout: float = 0.1):
        super(FeedForwardNetwork, self).__init__()
        self.linear1 = nn.Linear(d_model, d_ff)
        self.dropout = nn.Dropout(dropout)
        self.linear2 = nn.Linear(d_ff, d_model)
        self.relu = nn.ReLU()

    def forward(self, x):
        x = self.linear1(x)
        x = self.relu(x)
        x = self.dropout(x)
        x = self.linear2(x)
        return x  # (batch, seq_len, d_model)

Encoder stack

We have all the ingredient to put together the encoder stack by combining encoder layers $N=6$ times.

class EncoderLayer(nn.Module):
    def __init__(
        self,
        d_model: int,
        self_attention_block: MultiHeadAttention,
        feed_forward_block: FeedForwardNetwork,
        dropout: float,
    ):
        super().__init__()
        self.self_attention_block = self_attention_block
        self.feed_forward_block = feed_forward_block
        self.residual_connections = nn.ModuleList(
            [ResidualConnection(d_model, dropout) for _ in range(2)]
        )

    # src_mask is needed to be applied to the input of the encoder
    # to ensure padding words do not interact with actual words
    def forward(self, x, src_mask):
        x = self.residual_connections[0](
            x, lambda x: self.self_attention_block(x, x, x, src_mask)
        )
        x = self.residual_connections[1](x, self.feed_forward_block)
        return x


class EncoderStack(nn.Module):
    def __init__(self, d_model: int, layers: nn.ModuleList):
        super().__init__()
        self.layers = layers
        self.norm = LayerNormalization(d_model)

    def forward(self, x, mask):
        for layer in self.layers:
            x = layer(x, mask)
        return self.norm(x)

Decoder Stack

Create a decoder stack too.

class DecoderLayer(nn.Module):
    def __init__(
        self,
        d_model: int,
        self_attention_block: MultiHeadAttention,
        cross_attention_block: MultiHeadAttention,
        feed_forward_block: FeedForwardNetwork,
        dropout: float,
    ):
        super().__init__()
        self.self_attention_block = self_attention_block
        self.cross_attention_block = cross_attention_block
        self.feed_forward_block = feed_forward_block
        self.residual_connections = nn.ModuleList(
            [ResidualConnection(d_model, dropout) for _ in range(3)]
        )

    # src_mask coming from Encoder
    # tgt_mask coming from Decode
    def forward(self, x, encoder_output, src_mask, tgt_mask):
        x = self.residual_connections[0](
            x, lambda x: self.self_attention_block(x, x, x, tgt_mask)
        )
        # query comes from Decoder, but K and V come from Encoder
        x = self.residual_connections[1](
            x,
            lambda x: self.cross_attention_block(
                x, encoder_output, encoder_output, src_mask
            ),
        )
        x = self.residual_connections[2](x, self.feed_forward_block)
        return x


class DecoderStack(nn.Module):
    def __init__(self, d_model: int, layers: nn.ModuleList):
        super().__init__()
        self.layers = layers
        self.norm = LayerNormalization(d_model)

    def forward(self, x, encoder_output, src_mask, tgt_mask):
        for layer in self.layers:
            x = layer(x, encoder_output, src_mask, tgt_mask)
        return self.norm(x)

Projection Layer

Decoder stack will output vectors in embedding space (not words). Hence, we need to “project” these vectors back into words space to retrieve the words from the embedding vocabulary, which originally helped us map words (integers) into embeddings. This is done with a simple linear layer which is then followed by a softmax to get the probabilities.

class ProjectionLayer(nn.Module):
    def __init__(self, d_model, vocab):
        super().__init__()
        self.proj = nn.Linear(d_model, vocab)

    def forward(self, x):
        # log_softmax for numerical stability
        return torch.log_softmax(self.proj(x), dim=-1)  # (batch, seq_len, vocab)

Full Transformer

Finally, all pieces are put together to assemble the transformer!

class Transformer(nn.Module):
    def __init__(
        self,
        encoder: EncoderStack,
        decoder: DecoderStack,
        src_embed: Embeddings,
        tgt_embed: Embeddings,
        src_pos: PE,
        tgt_pos: PE,
        projection_layer: ProjectionLayer,
    ):
        super().__init__()
        self.encoder = encoder
        self.decoder = decoder
        self.src_embed = src_embed
        self.tgt_embed = tgt_embed
        self.src_pos = src_pos
        self.tgt_pos = tgt_pos
        self.projection_layer = projection_layer

    def encode(self, src, src_mask):
        src = self.src_embed(src)
        src = self.src_pos(src)
        return self.encoder(src, src_mask)  # (batch, seq_len, d_model)

    def decode(
        self, encoder_output: Tensor, src_mask: Tensor, tgt: Tensor, tgt_mask: Tensor
    ):
        tgt = self.tgt_embed(tgt)
        tgt = self.tgt_pos(tgt)
        return self.decoder(
            tgt, encoder_output, src_mask, tgt_mask
        )  # (batch, seq_len, d_model)

    def project(self, x):
        return self.projection_layer(x)  # (batch, seq_len, vocab)