Import MNIST
Let’s download $7000$ examples of length $784 = 28\times 28$ of flattened grayscale square images of handwritten digits, stacked as a tuple of $(X,Y)$ with Python shapes $(70000, 784)$ and $(70000,).$
from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784', return_X_y= True)
Convert them to allowed formats and do the train-test $(5:2)$ split.
import numpy as np
X = np.float32(mnist[0]/256) # (70000, 784)
Y = np.int64(mnist[1]) # (70000,)
x_train,y_train,x_valid,y_valid = X[:50000,:],Y[:50000],X[50000:,:],Y[50000:]
Take a look at the first training example!
import matplotlib.pyplot as plt
plt.imshow(x_train[0].reshape((28, 28)), cmap="gray")
DataLoader
Some technical steps
- Convert the data to “torch tensors”
- Form a DataLoader (to simplify the iteration process over batches)
Notice that no shuffling is required for the validation data
import torch
x_train, y_train, x_valid, y_valid = map(torch.tensor,
(x_train, y_train, x_valid, y_valid))
from torch.utils.data import TensorDataset
train_ds = TensorDataset(x_train, y_train)
valid_ds = TensorDataset(x_valid, y_valid)
from torch.utils.data import DataLoader
train_dl = DataLoader(train_ds, batch_size=64, shuffle=True)
valid_dl = DataLoader(valid_ds, batch_size=128)
Model, Optimizer & Loss
Lets design the NN architecture by subclassing nn.Module , which manages the network parameters/weights, their gradients, etc. Create a simple linear layer self.lin = nn.Linear(784, 10) which implicitly is equivalent to creating a $784\times 10$ matrix of weights and a $10$-dim bias vector
self.weights = nn.Parameter(torch.randn(784, 10) / math.sqrt(784))
self.bias = nn.Parameter(torch.zeros(10))
Both parameters are initially random, Xavier initialized, but need to be determined eventually. For now, let’s not add any nonlinearities. Also incorporate the forward step, which will multiply the input by the matrix and add the bias, xb @ self.weights + self.bias . Hence we have
from torch import nn
class FeedForward(nn.Module):
def __init__(self):
super().__init__()
self.lin = nn.Linear(784, 10)
def forward(self, xb):
return self.lin(xb)
model = FeedForward()
Pick the optimizer and the learning rate.
from torch import optim
opt = optim.Adam(model.parameters(), lr=.001)
Specify the loss. F.cross_entropy combines negative log likelihood loss and log softmax activation and works well for classification purposes.
import torch.nn.functional as F
loss_func = F.cross_entropy
Training
Iterate over all training images $15$ times, each time sampling batches from DataLoader.
For each batch,
- Make a prediction
model(xb), which propagatesxbforward. - Compute the loss
loss_func(pred, yb) - Propagate backwards:
- Update the gradients
- Optimize the weights, i.e. for each parameter
pdop -= p.grad * lr - Reset the gradient back to $0$ so it is ready for the next batch
for epoch in range(15):
for xb, yb in train_dl:
pred = model(xb)
loss = loss_func(pred, yb) # pred.dtype=torch.float32, yb.dtype=torch.int64
loss.backward()
opt.step()
opt.zero_grad()
print(loss_func(model(xb), yb))
Validation
Easy to check the validation loss too (the lines model.train() and model.eval() ensure appropriate behavior in more complex cases)
for epoch in range(15):
model.train() # NEW
for xb, yb in train_dl:
pred = model(xb)
loss = loss_func(pred, yb)
loss.backward()
opt.step()
opt.zero_grad()
# Validation
model.eval() # NEW
with torch.no_grad():
valid_loss = sum(loss_func(model(xb), yb).tolist() for xb, yb
in valid_dl)/ len(valid_dl)
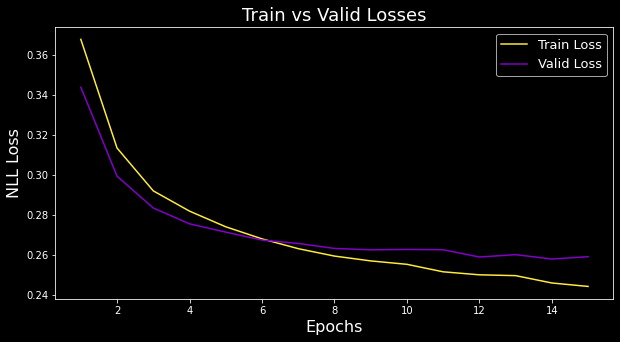
Can also plot both losses over epochs
Make a prediction
Plot a few validation images
fig = plt.figure(figsize=(3, 3))
rows, cols = 3,3
for i in range(0, cols*rows):
fig.add_subplot(rows, cols, i+1)
plt.imshow(x_valid[i].reshape((28, 28)), cmap="gray") # True
plt.show()
print(torch.argmax(model(x_valid[0:9]), axis=1).reshape(3,3)) # Pred
 vs $\begin{matrix} [3, 8, 6]\\ [9, 6, 4]\\ [5, 3, 8] \end{matrix}$
vs $\begin{matrix} [3, 8, 6]\\ [9, 6, 4]\\ [5, 3, 8] \end{matrix}$
CNN
Can use a Convolutional NN instead. Our inputs are $28\times 28\times 1$, where $1$ is the # of channels (only gray).
The first two arguments of Conv2d are in_channels=1 and out_channels=16.
A useful formula for keeping track of dimensions is
\[n_{out} = \frac{n_{in} - k + 2p}{s} + 1\]where $n$ is image’s spatial dimension (height or weight).
Conv2d(1,16,3,2,1): 28x28x1 (28-3+2)/2+1 = 14.5 14x14x16Conv2d(16,16,3,2,1): 14x14x16 (14-3+2)/2+1 = 7.5 7x7x16Conv2d(16,10,3,2,1): 7x7x16 (7-3+2)/2+1 = 4 4x4x10avg_pool2d(xb,4): 4x4x10 1x10
class CNN(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1, 16, kernel_size=3, stride=2, padding=1)
self.conv2 = nn.Conv2d(16, 16, kernel_size=3, stride=2, padding=1)
self.conv3 = nn.Conv2d(16, 10, kernel_size=3, stride=2, padding=1)
def forward(self, xb):
xb = xb.view(-1, 1, 28, 28)
xb = F.relu(self.conv1(xb))
xb = F.relu(self.conv2(xb))
xb = F.relu(self.conv3(xb))
xb = F.avg_pool2d(xb, 4)
return xb.view(-1, xb.size(1))
model = CNN()
Full Code for CNN
# Import Data
from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784', return_X_y= True)
import numpy as np
X = np.float32(mnist[0]/256) # (70000, 784)
Y = np.int64(mnist[1]) # (70000,)
x_train,y_train,x_valid,y_valid = X[:50000,:],Y[:50000],X[50000:,:],Y[50000:]
import matplotlib.pyplot as plt
plt.imshow(x_train[0].reshape((28, 28)), cmap="gray")
# Use DataLoader
import torch
x_train, y_train, x_valid, y_valid = map(torch.tensor,
(x_train, y_train, x_valid, y_valid))
from torch.utils.data import TensorDataset
train_ds = TensorDataset(x_train, y_train)
valid_ds = TensorDataset(x_valid, y_valid)
from torch.utils.data import DataLoader
train_dl = DataLoader(train_ds, batch_size=64, shuffle=True)
valid_dl = DataLoader(valid_ds, batch_size=128)
# Set up architecture
from torch import nn
class CNN(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1, 16, kernel_size=3, stride=2, padding=1)
self.conv2 = nn.Conv2d(16, 16, kernel_size=3, stride=2, padding=1)
self.conv3 = nn.Conv2d(16, 10, kernel_size=3, stride=2, padding=1)
def forward(self, xb):
xb = xb.view(-1, 1, 28, 28)
xb = F.relu(self.conv1(xb))
xb = F.relu(self.conv2(xb))
xb = F.relu(self.conv3(xb))
xb = F.avg_pool2d(xb, 4)
return xb.view(-1, xb.size(1))
model = CNN()
# Optimizer
from torch import optim
opt = optim.Adam(model.parameters(), lr=.001)
# Loss
import torch.nn.functional as F
loss_func = F.cross_entropy
# Training
for epoch in range(15):
model.train()
for xb, yb in train_dl:
pred = model(xb)
loss = loss_func(pred, yb)
loss.backward()
opt.step()
opt.zero_grad()
# Validation
model.eval()
with torch.no_grad():
valid_loss = sum(loss_func(model(xb), yb).tolist() for xb, yb
in valid_dl)/ len(valid_dl)
print(epoch, valid_loss)
# True vs Pred
fig = plt.figure(figsize=(3, 3))
rows, cols = 3,3
for i in range(0, cols*rows):
fig.add_subplot(rows, cols, i+1)
plt.imshow(x_valid[i].reshape((28, 28)), cmap="gray") # True
plt.show()
print(torch.argmax(model(x_valid[0:9]), axis=1).reshape(3,3)) # Pred